树结构 https://www.cnblogs.com/crazymakercircle/p/16320430.html

R 树.md

原文链接： https://zhuanlan.zhihu.com/p/62639268

R 树的数据结构

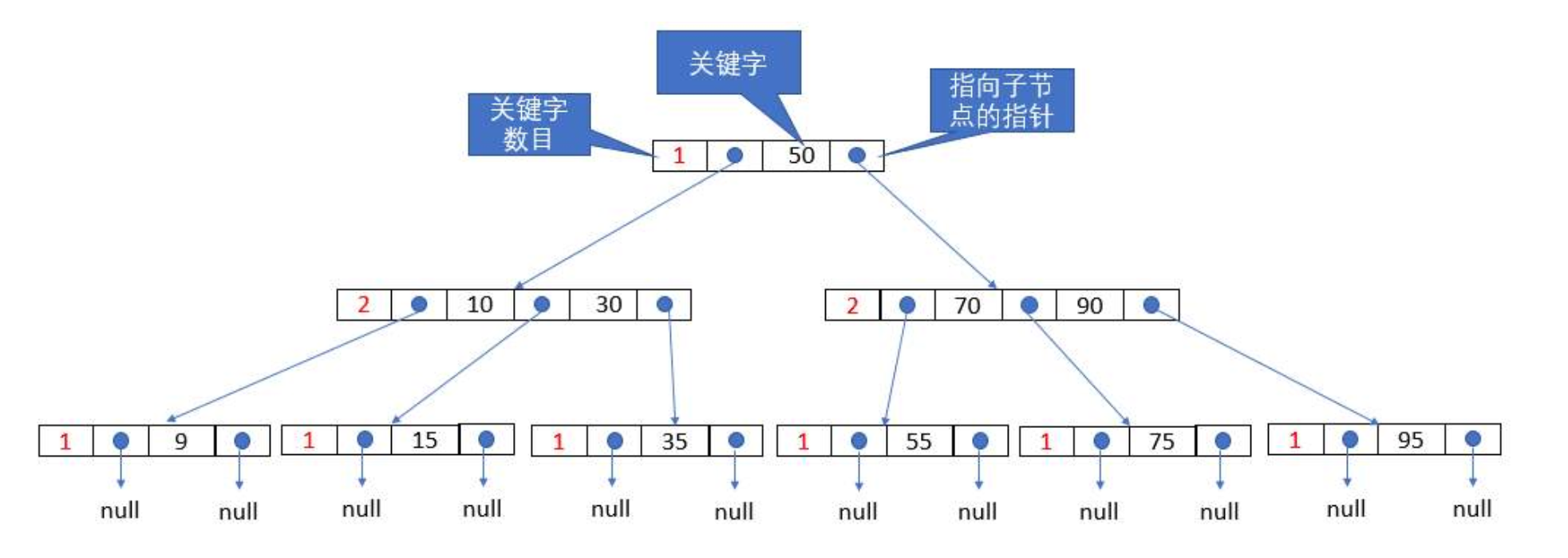
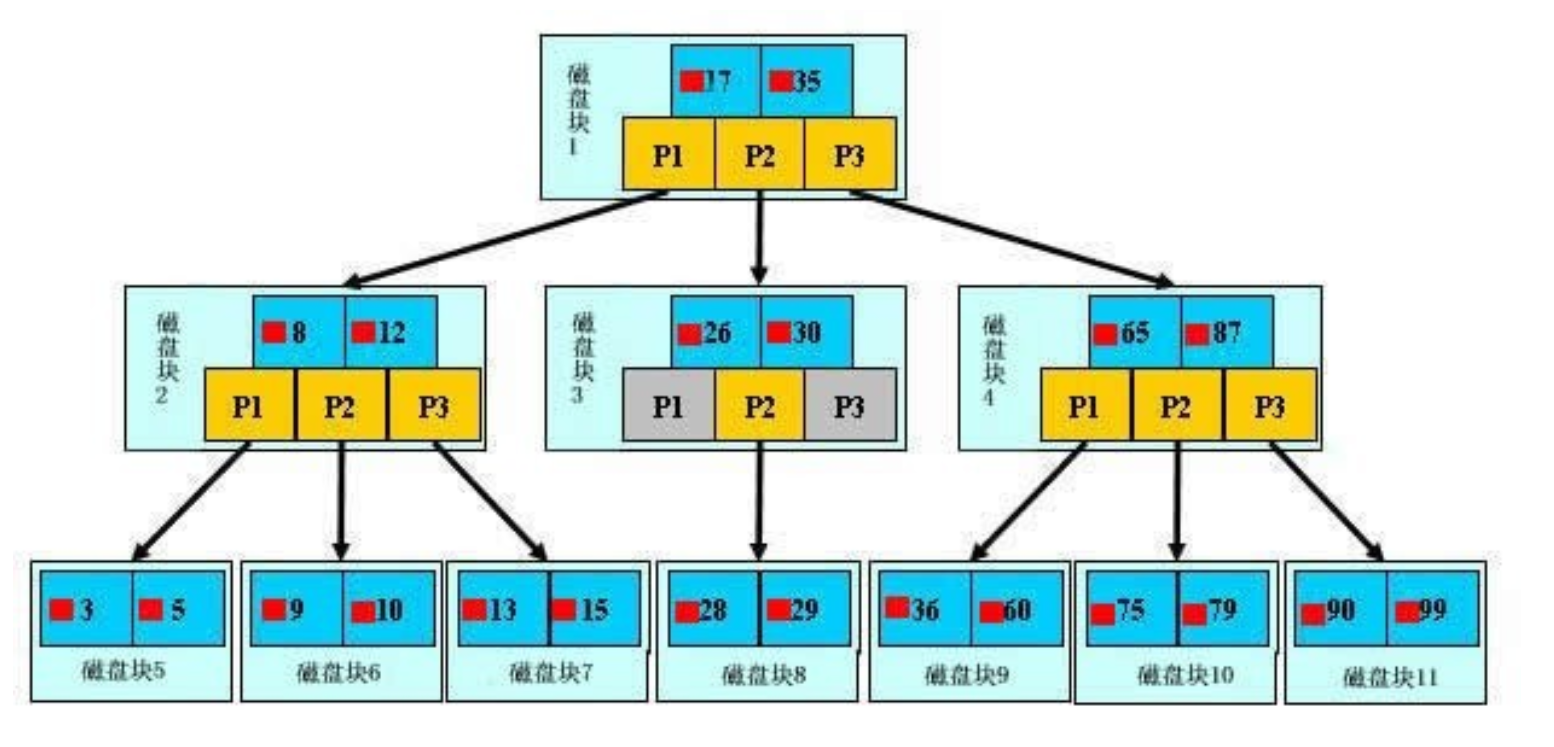
R树是B树在高维空间的扩展，是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。

根据R树的这种数据结构，当我们需要进行一个高维空间查询时，我们只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足要求即可。

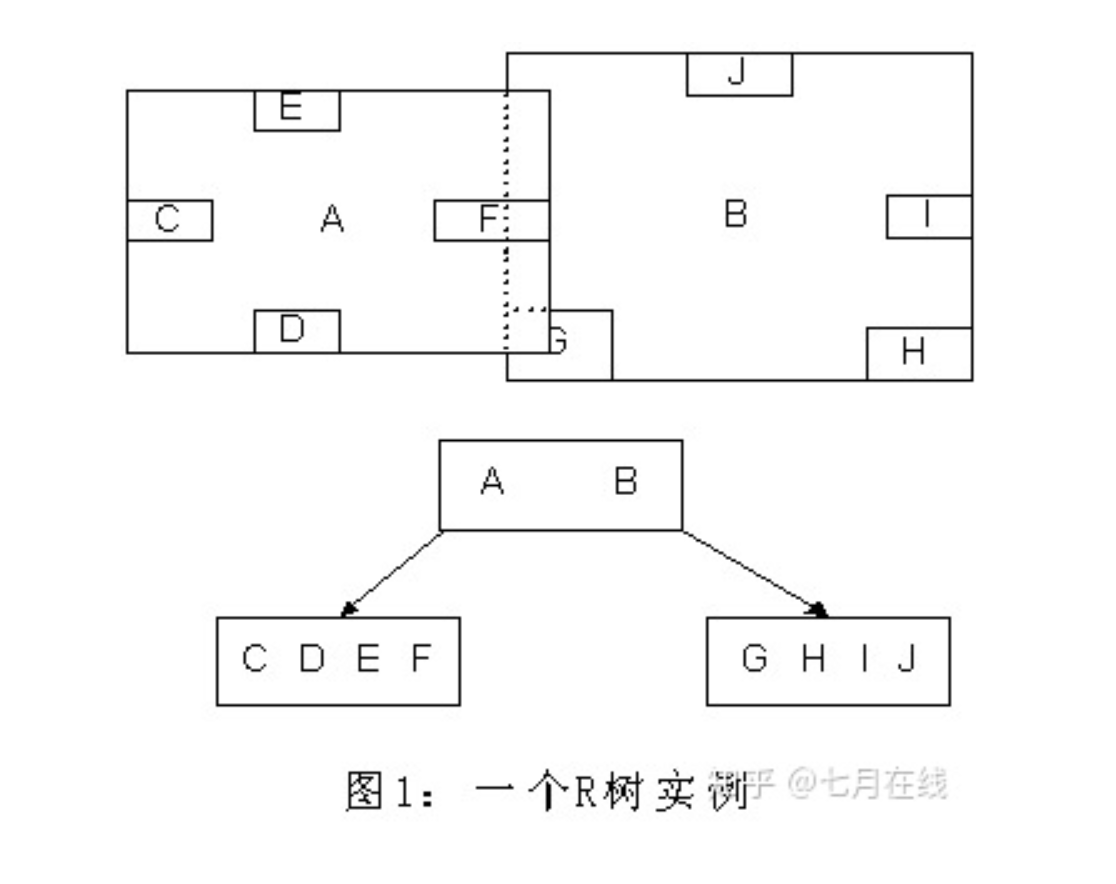
这种方式使我们不必遍历所有数据即可获得答案，效率显著提高。下图1是R树的一个简单实例：

我们在上面说过，R树运用了空间分割的理念，这种理念是如何实现的呢？R树采用了一种称为MBR(Minimal Bounding Rectangle)的方法，在此我把它译作“最小边界矩形”。

从叶子结点开始用矩形（rectangle）将空间框起来，结点越往上，框住的空间就越大，以此对空间进行分割。有点不懂？没关系，继续往下看。

在这里我还想提一下，R树中的R应该代表的是Rectangle（此处参考wikipedia上关于R树的介绍），而不是大多数国内教材中所说的Region（很多书把R树称为区域树，这是有误的）。

我们就拿二维空间来举例。下图是Guttman论文中的一幅图：

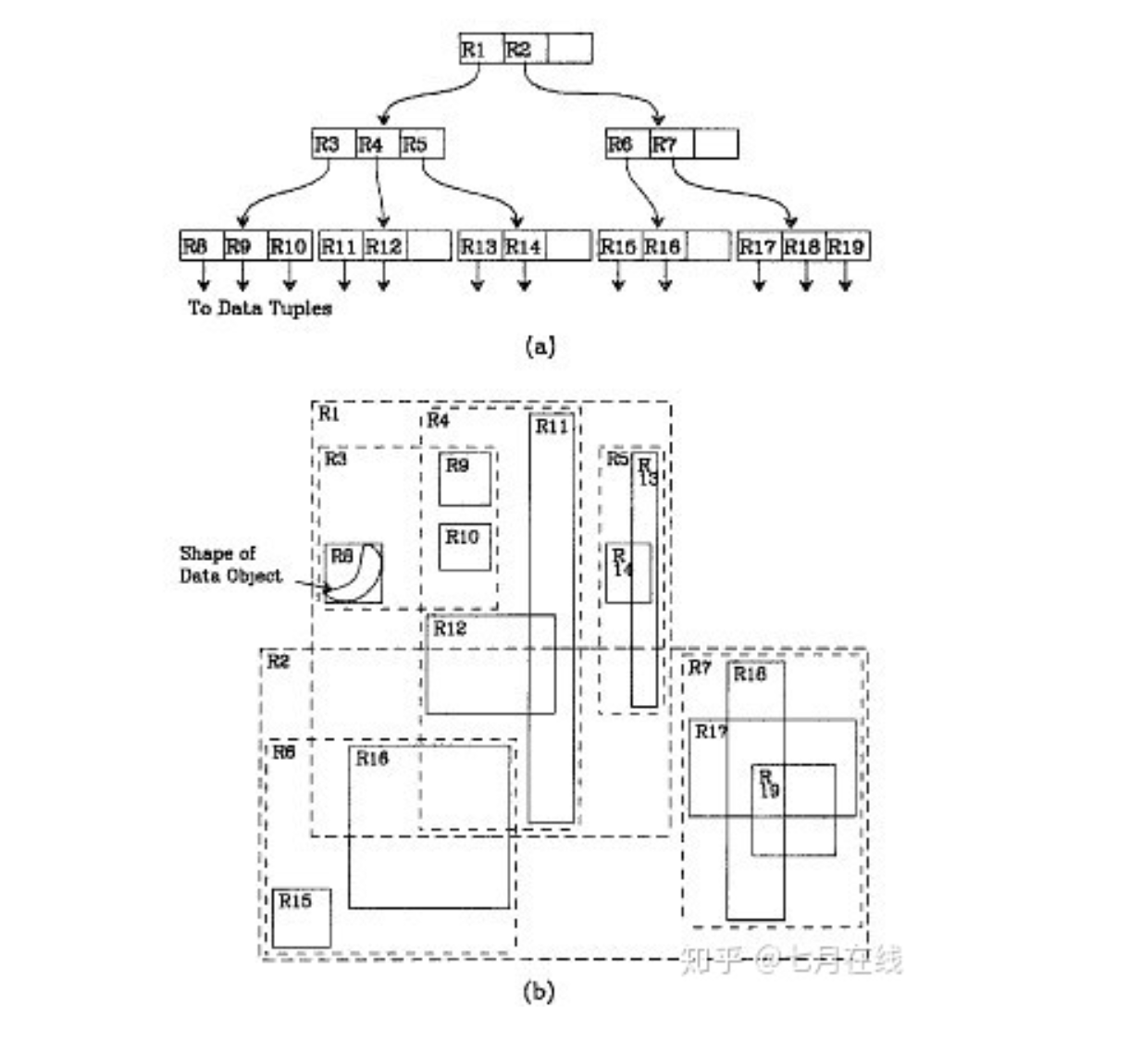
我来详细解释一下这张图。

先来看图（b）

A）首先我们假设所有数据都是二维空间下的点，图中仅仅标志了R8区域中的数据，也就是那个shape of data object。别把那一块不规则图形看成一个数据，我们把它看作是多个数据围成的一个区域。

为了实现R树结构，我们用一个最小边界矩形恰好框住这个不规则区域，这样，我们就构造出了一个区域：R8。R8的特点很明显，就是正正好好框住所有在此区域中的数据。其他实线包围住的区域，如R9，R10，R12等都是同样的道理。

这样一来，我们一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。

B）下一步操作就是进行高一层次的处理。我们发现R8，R9，R10三个矩形距离最为靠近，因此就可以用一个更大的矩形R3恰好框住这3个矩形。

C）同样道理，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。

我想大家都应该理解这个数据结构的特征了。用地图的例子来解释，就是所有的数据都是餐厅所对应的地点，先把相邻的餐厅划分到同一块区域，划分好所有餐厅之后，再把邻近的区域划分到更大的区域，划分完毕后再次进行更高层次的划分，直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。

下面就可以把这些大大小小的矩形存入我们的R树中去了。根结点存放的是两个最大的矩形，这两个最大的矩形框住了所有的剩余的矩形，当然也就框住了所有的数据。下一层的结点存放了次大的矩形，这些矩形缩小了范围。每个叶子结点都是存放的最小的矩形，这些矩形中可能包含有n个数据。

在这里，读者先不要去纠结于如何划分数据到最小区域矩形，也不要纠结怎样用更大的矩形框住小矩形，这些都是下一节我们要讨论的。

讲完了基本的数据结构，我们来讲个实例，如何查询特定的数据。又以餐厅为例，假设我要查询广州市天河区天河城附近一公里的所有餐厅地址怎么办？

1 打开地图（也就是整个R树），先选择国内还是国外（也就是根结点）。

2 然后选择华南地区（对应第一层结点），选择广州市（对应第二层结点），

3 再选择天河区（对应第三层结点），

4 最后选择天河城所在的那个区域（对应叶子结点，存放有最小矩形），遍历所有在此区域内的结点，看是否满足我们的要求即可。

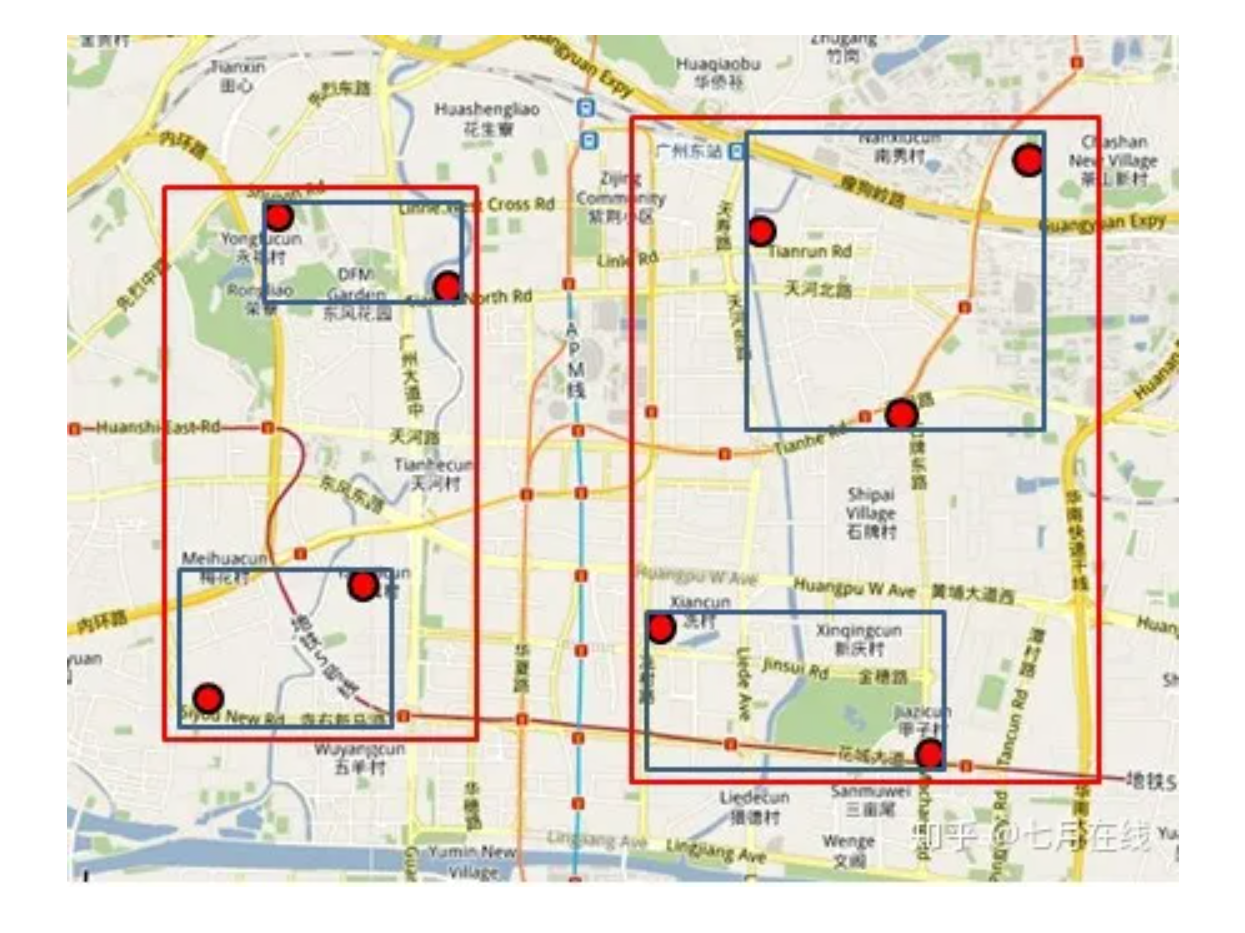
怎么样，其实R树的查找规则跟查地图很像吧？对应下图：

一棵R树满足如下的性质：

1. 除非它是根结点之外，所有叶子结点包含有m至M个记录索引（条目）。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。

2. 对于所有在叶子中存储的记录（条目），I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（注意：此处所说的“矩形”是可以扩展到高维空间的）。

3. 每一个非叶子结点拥有m至M个孩子结点，除非它是根结点。

4. 对于在非叶子结点上的每一个条目，i是最小的可以在空间上完全覆盖这些条目所代表的店的矩形（同性质2）。

5. 所有叶子结点都位于同一层，因此R树为平衡树。

叶子结点的结构

先来探究一下叶子结点的结构。叶子结点所保存的数据形式为：(I, tuple-identifier)。

其中，tuple-identifier表示的是一个存放于数据库中的tuple，也就是一条记录，它是n维的。I是一个n维空间的矩形，并可以恰好框住这个叶子结点中所有记录代表的n维空间中的点。I=(I0,I1,…,In-1)。其结构如下图所示：

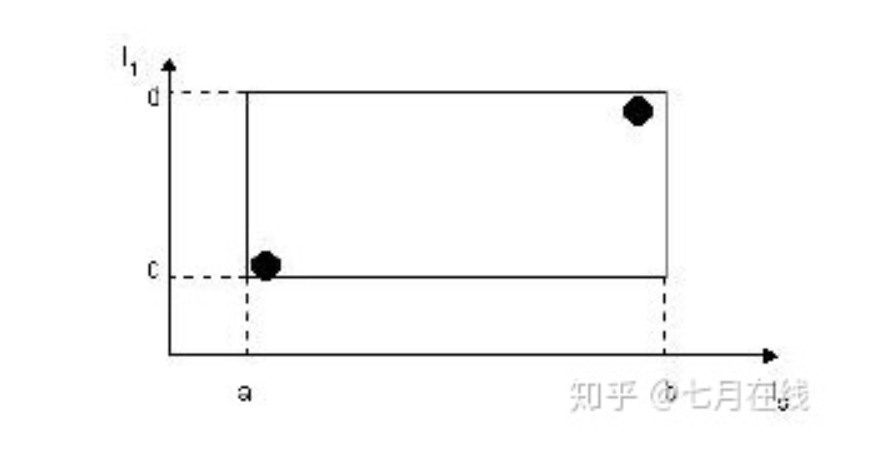
下图描述的就是在二维空间中的叶子结点所要存储的信息。

在这张图中，I所代表的就是图中的矩形，其范围是a<=I0<=b，c<=I1<=d。有两个tuple-identifier，在图中即表示为那两个点。这种形式完全可以推广到高维空间。大家简单想想三维空间中的样子就可以了。这样，叶子结点的结构就介绍完了。

非叶子结点

非叶子结点的结构其实与叶子结点非常类似。想象一下B树就知道了，B树的叶子结点存放的是真实存在的数据，而非叶子结点存放的是这些数据的“边界”，或者说也算是一种索引（有疑问的读者可以回顾一下上述第一节中讲解B树的部分）。

同样道理，R树的非叶子结点存放的数据结构为：(I, child-pointer)。

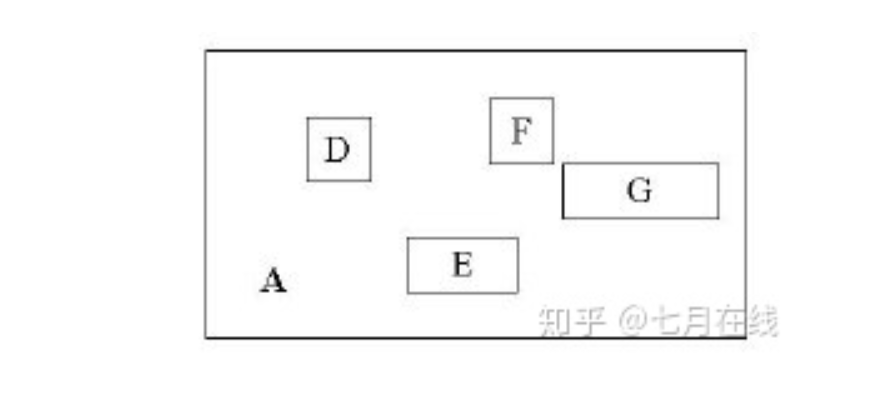
其中，child-pointer是指向孩子结点的指针，I是覆盖所有孩子结点对应矩形的矩形。这边有点拗口，但我想不是很难懂？给张图：

D,E,F,G为孩子结点所对应的矩形。A为能够覆盖这些矩形的更大的矩形。这个A就是这个非叶子结点所对应的矩形。

这时候你应该悟到了吧？无论是叶子结点还是非叶子结点，它们都对应着一个矩形。树形结构上层的结点所对应的矩形能够完全覆盖它的孩子结点所对应的矩形。根结点也唯一对应一个矩形，而这个矩形是可以覆盖所有我们拥有的数据信息在空间中代表的点的。

我个人感觉这张图画的不那么精确，应该是矩形A要恰好覆盖D,E,F,G，而不应该再留出这么多没用的空间了。但为尊重原图的绘制者，特不作修改。

数据结构和算法.md

原文连接：https://www.cnblogs.com/yanghh/p/14132710.html

B 树 和 B+ 树

B 树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树，多叉就是多个分支的意思，二叉树就是最多只有两个分支的树。

如下图所示，即是一棵 B 树。

一棵 m 阶的 B 树必须满足如下条件：

1）每个结点最多含有 m 个分支，也就是说：每个节点最多 m−1 个关键字。

2）根节点最少可以有 1 个关键字，其它节点最少有 ⌈m2⌉−1 个关键字。

3）每个节点的内部结构为：n 为节点中关键字的个数，Ki,i=1,2,...,n 为关键字，从小到大排列，Pi,i=0,1,...,n 为指向关键字满足 [Ki,Ki+1] 范围的孩子节点。

这里认为上面的 B 树高度为 3，第三层就是叶子节点，至于有些材料说那些 null 是叶子节点，简直扯淡。

B 树的节点类型定义如下，这个定义只是用来查找内存数据的，如果用来查找外存，代码需要调整一下，下面叙述。

typedef int KeyType;
 
struct BTNode {
    int keyNum;              // 关键字个数
    struct BTNode *parent;   // 指向父节点
    struct BTNode **ptr;     // 子树指针向量, ptr[0],ptr[1],...,ptr[keyNum]
    KeyType **key;           // 关键字向量, key[0],key[1],...,key[keyNum-1]
}

B 树设计的目的是用来查找磁盘的，为了简单，假设每个盘块正好存放一个 B 树的结点,这里用少量数据构造一棵 3 叉树的形式，来描述文件查找的具体过程。

上面的图中比如根结点，其中 17 表示一个磁盘文件的文件名；小红方块表示这个 17 文件内容在硬盘中的存储位置；P1 表示指向 17 左子树的指针。

此时节点类型定义如下：

typedef char* KeyType;
 
struct BTNode {
    int keyNum;              // 关键字个数
    struct BTNode *parent;   // 指向父节点
    struct BTNode **ptr;     // 子树指针向量, ptr[0],ptr[1],...,ptr[keyNum]，每个元素存放另外一个盘块的地址
    KeyType **key;           // 关键字向量, 存储的是文件名
    FILE_HARD_ADDR *offset;  // 存储每个文件(关键字)的磁盘地址
}

下面来模拟下查找文件 29 的过程：

1）根据根结点指针找到文件目录的根磁盘块 1，将其中的信息导入内存。【磁盘 IO 操作 1 次】 

2）此时内存中有两个文件名 17、35 和三个存储其他磁盘页面地址的数据。根据算法我们发现：17<29<35，因此我们找到指针 P2。

3）根据 P2 指针，我们定位到磁盘块 3，并将其中的信息导入内存。【磁盘 IO 操作 2 次】

4）此时内存中有两个文件名 26、30 和三个存储其他磁盘页面地址的数据。根据算法我们发现：26<29<30，因此我们找到指针 P2。

5）根据 P2 指针，我们定位到磁盘块 8，并将其中的信息导入内存。【磁盘 IO 操作 3 次】

6）此时内存中有两个文件名 28、29。根据算法我们查找到文件名 29，并定位了该文件内存的磁盘地址。

分析上面的过程，发现需要 3 次磁盘 IO 操作和 3 次内存查找操作。关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率。

至于 IO 操作是影响整个 B 树查找效率的决定因素。

根据上面的例子我们可以看出，对于辅存做 IO 读的次数取决于 B 树的高度。而 B 树的高度由什么决定的呢？

简单树的概念.md

树

树的概念：

1. 只有一个根节点
2. 除了根节点，所有节点有且只有一个父节点，可以有 0 个或者多个子节点
3. 树是无环的

二叉树

二叉树的概念：每个节点最多有两个节点的树称之为二叉树。

满二叉树和完全二叉树

满二叉树：所有的节点都有两个节点。

完全二叉树：深度为 h 具有 n 个节点的二叉树，它的每个节点必须与深度为 h 的满二叉树的前 n 个节点位置对应。

二叉查找树（二叉搜索树）

一个二叉查找树必须满足以下条件：

1. 所有节点都有一个属性可以用来两两间比较
2. 任意节点必须大于它的左子树上所有节点，小于它的右子树上的所有节点

二叉查找树正因为有以上特性，改善了查找算法的效率。